文案 | 轉(zhuǎn)錄調(diào)控事業(yè)部
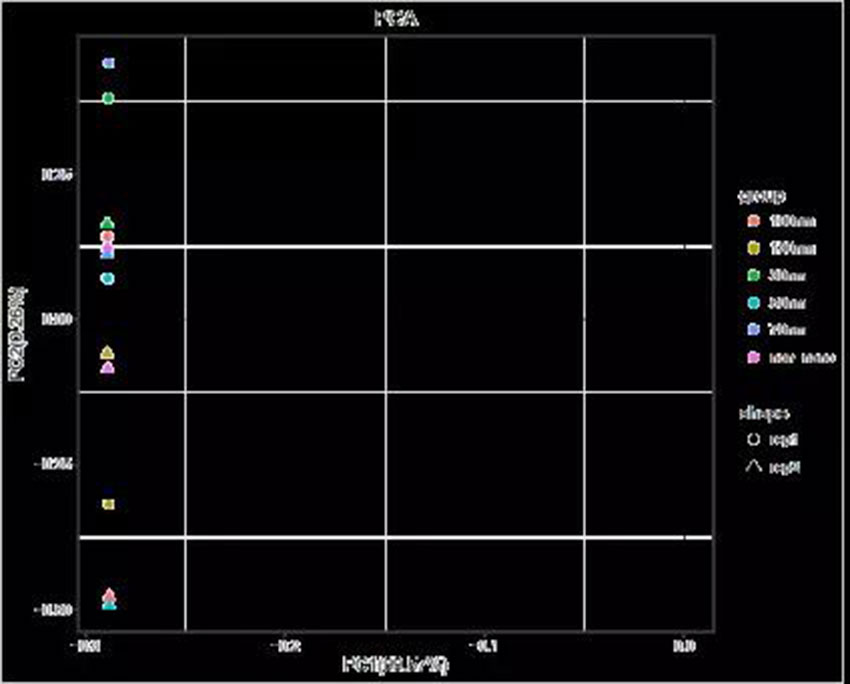
小伙伴兒們在拿到轉(zhuǎn)錄組結(jié)題報告后�,會發(fā)現(xiàn)一張名為PCA的主成分分析圖,如下所示:
PCA圖到底代表什么意義��?是怎么得到的����?
今天我們一一闡明。
PCA(Principal Component Analysis)官方定義如下:
是一種通過線性變換將原始數(shù)據(jù)變換為一組各維度線性無關(guān)表示的數(shù)據(jù)分析方法�����。
對于沒有相關(guān)背景的童鞋們來說,看完定義好像更加摸不著頭腦了��。讓我們先用社會通用語翻譯一下這個定義:PCA算法主要是用于提取大數(shù)據(jù)的主要特征分量�����,又稱為主成分分析���。
那主成分又是什么概念呢����?
要搞明白數(shù)據(jù)的主成分�����,就不得不從數(shù)據(jù)降維說起���。數(shù)據(jù)降維也是PCA分析的思想。
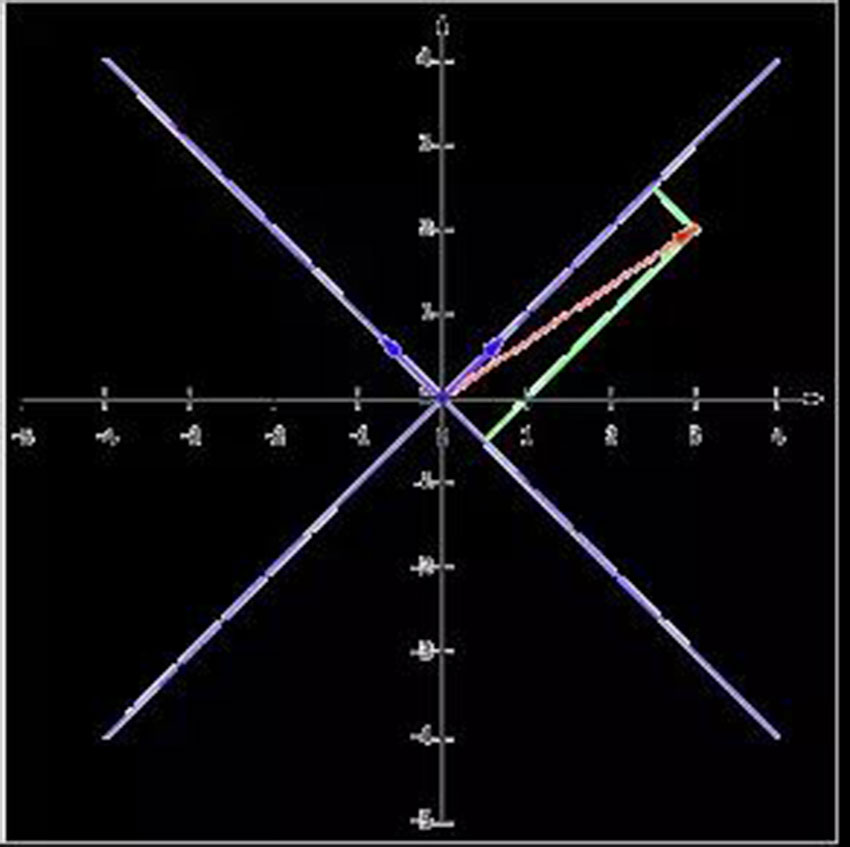
舉個簡單直觀的例子:假設(shè)三維空間中有一系列點,這些點分布在一個過原點的斜面上����,如果用自然坐標(biāo)系x,y,z這三個軸來表示這組數(shù)據(jù)的話�����,需要使用三個維度。這時我們把x,y,z坐標(biāo)系旋轉(zhuǎn)一下,使數(shù)據(jù)所在平面與x,y平面重合,把旋轉(zhuǎn)后的坐標(biāo)系記為x',y',z'�,那么這組數(shù)據(jù)的表示只用x'和y'兩個維度表示即可����。即從三維降到了二維�。
我們都知道,三點一定共面,也就是說三維空間中任意三點中心化后都是線性相關(guān)的,按照這個思路而言,n維空間中的n個點一定能在一個k(k<n)維空間中分析����。
降維意味著信息的丟失����,為了盡力將信息的損失盡量降低�����,我們鑒于實際數(shù)據(jù)本身常常存在的相關(guān)性���,可以選擇k維空間中累計貢獻度最大的前兩個向量作為數(shù)據(jù)源進行降維分析��,最終得到主成分Y1、Y2���,主成分定義如下:
設(shè)X =( x1, x2,…… xp)’是p維隨機向量,二階矩存在��。若向量t1’=(*11�����,*12……t*1P) 在|t1|= 1的條件下使得Varp(t'1X) 最大, 則稱Y1 =t'1X 是X的第一主成分或第一主分量; 若向量t2’=(*21,*22……t*2P)在|t2|=1; Cov(t'2X, Y1)=0的條件下使得Varp(t'2X) 最大����,則稱Y2 =t'2X 是X的第二主成分或第二主分量���。
好了�����,理論知識準(zhǔn)備好了,回到我們最初的目的上來�����,我們拿到了一組轉(zhuǎn)錄組數(shù)據(jù)��,每一個檢測到的基因都有一個表達量數(shù)值(FPKM/RPKM/TPM)��,所有基因的表達量都在二維空間中轉(zhuǎn)化為一組向量����,假設(shè)我們此次檢測到一萬個基因����,那理論上全部數(shù)據(jù)的空間分布可能涉及到一萬個維度,根據(jù)我們的降維思路�����,n維空間中的n個點一定能在一個k(k<n)維空間中分析����,我們就可以通過線性變換將高維數(shù)據(jù)最終壓縮到第一��、第二特征分量所在的二維平面上�,最終得到我們看到的以PC1��、PC2展示的圖片效果����。
關(guān)于PCA的降維思想�,你get到了嗎?