
2024-10-10

隨著質譜技術(Mass Spectrometry, MS)的飛速發展,基于Astral質譜儀的蛋白質組學越來越受到學術界關注,由于其高掃描速度、超高分辨率、超高靈敏度的儀器性質使得蛋白質組學數據變得越來越復雜和龐大,這對數據分析和解讀提出了更高的要求。為了從海量數據中提取有價值的信息,統計檢驗方法成為蛋白質組學數據分析的核心工具。小編將詳細介紹并比較幾種常用的蛋白質組學統計檢驗方法,幫助大家理解這些方法在蛋白質組學研究中的重要性及其適用場景。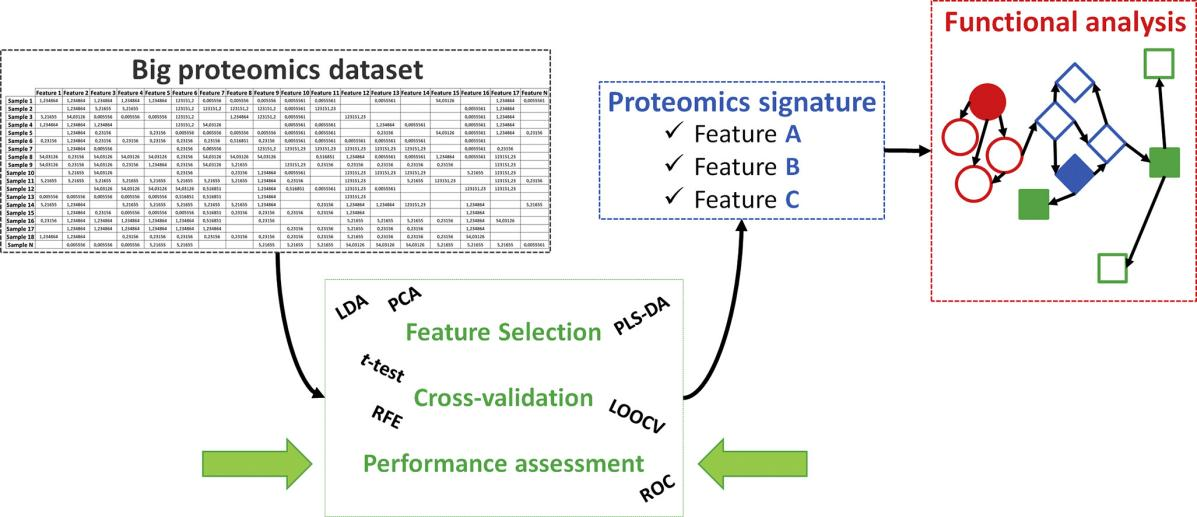
一. 參數檢驗
參數檢驗是基于樣本數據符合特定分布(通常是正態分布)的假設,進而對樣本的均值、方差等參數進行顯著性檢驗。 1.1、檢驗(T-test) 原理 t檢驗是一種用于比較兩組樣本均值是否顯著不同的經典統計方法。在蛋白質組學中,t檢驗常用于不同條件(如對照組和處理組)下蛋白質豐度的差異分析。t檢驗基于假設樣本數據服從正態分布,因此適用于正態分布的數據集。 常見t檢驗類型 獨立樣本t檢驗:用于比較兩組獨立樣本(如對照組與實驗組)的均值差異。在蛋白質組學研究中,可以用來比較不同處理條件下某些蛋白質的豐度變化。 配對樣本t檢驗:用于比較同一組樣本在不同條件下(如處理前和處理后)的差異。例如,分析藥物處理前后同一批樣本中蛋白質的變化。 優點 t檢驗是一種簡便且廣泛使用的統計方法,適用于小規模樣本數據的比較,計算簡單,易于理解。 缺點 t檢驗對數據正態性要求較高,如果數據不符合正態分布,可能會影響結果的準確性。因此,使用前需要對數據進行分布測試或使用非參數方法替代。 應用場景 t檢驗常用于蛋白質組學中的定量分析,特別是當研究者僅關注兩組條件(如疾病組和健康組)的差異時。它能夠幫助確定哪些蛋白質在兩種條件下表現出顯著的表達變化。如果p值小于顯著性水平(通常為0.05),則拒絕原假設,認為兩個樣本均值顯著不同。 1.2、方差分析(ANOVA) 原理 方差分析(ANOVA,Analysis of Variance)用于比較三組或更多組樣本均值是否存在顯著差異。與t檢驗不同,ANOVA能夠處理多個組別的數據,因此在蛋白質組學中常用于多組樣本的差異分析。ANOVA的核心在于分析組間方差與組內方差的比值。ANOVA通過計算F統計量,即組間方差與組內方差的比值,來評估組均值之間的差異是否顯著。 常見ANOVA類型 單因素ANOVA:分析一個因素(如處理時間)對蛋白質豐度的影響,比較多組樣本之間的差異。 多因素ANOVA:分析多個因素(如處理類型和時間)對蛋白質豐度的聯合影響。多因素ANOVA能夠處理復雜實驗設計,特別是當研究者需要同時考慮多種變量時。 優點 ANOVA能處理多個組別的數據,特別適用于復雜的實驗設計。它能夠檢測多個樣本組之間的差異,幫助研究者在多重實驗條件下分析蛋白質豐度的變化。 缺點 ANOVA假設數據的方差相等,如果方差不等,需要使用修正的方差分析方法。此外,ANOVA只能夠檢測組間是否存在差異,而無法指出具體哪些組之間存在顯著差異,因此需要后續的多重比較檢驗。 應用場景 ANOVA常用于蛋白質組學研究中涉及多組樣本的實驗設計,如不同時間點、不同劑量下的蛋白質豐度分析。它能夠有效地評估不同條件下蛋白質表達的整體趨勢。
二. 非參數檢驗
非參數檢驗是指不依賴于數據的特定分布假設的統計檢驗方法,主要用于當數據不服從正態分布或者樣本量較小時。蛋白質組學數據往往因其復雜性和多變性,常常無法滿足正態分布等假設,這時非參數檢驗就成為一個重要的分析工具。常見的非參數檢驗方法有Mann-Whitney U檢驗、Wilcoxon符號秩檢驗和Kruskal-Wallis檢驗等。 2.1、Mann-Whitney U檢驗 原理 Mann-Whitney U檢驗是一種非參數方法,用于比較兩組獨立樣本的分布差異。與t檢驗不同,它不依賴于數據的正態分布假設,因此適用于分布不對稱、含有異常值或不滿足方差齊性假設的數據集。該檢驗通過將兩組數據排序并比較它們的秩值來判斷兩組樣本是否來自相同的分布。 優點 Mann-Whitney U檢驗不依賴數據的正態分布,因此適合于非正態分布數據。即使樣本量較小,該檢驗依然能夠提供穩健的分析結果。該方法對異常值和數據噪聲不敏感。 缺點 Mann-Whitney U檢驗僅能用于兩組獨立樣本的比較,無法用于多組樣本。對于大樣本量且接近正態分布的數據,Mann-Whitney U檢驗的統計效能低于t檢驗。 應用場景 Mann-Whitney U檢驗廣泛應用于蛋白質組學中兩組獨立樣本的比較,特別適用于數據不符合正態分布或包含異常值的情況。例如,比較疾病組與健康組蛋白質豐度的差異,或者比較兩種不同處理條件下的蛋白質表達水平。 2.2、Wilcoxon符號秩檢驗 原理 Wilcoxon符號秩檢驗是另一種非參數檢驗方法,主要用于配對樣本的比較。該方法是t檢驗的非參數對應形式,適用于比較同一組樣本在不同條件下的差異。Wilcoxon符號秩檢驗通過計算每對樣本的差異,并將這些差異排序后進行符號和秩值的分析,以判斷兩種處理之間是否存在顯著差異。 優點 Wilcoxon符號秩檢驗特別適合用于比較配對樣本,如同一組樣本在處理前后或不同時間點的差異。該檢驗不需要假設數據服從正態分布,因此在數據不滿足正態性假設時比配對t檢驗更具優勢。Wilcoxon符號秩檢驗對于小樣本數據也有較好的適用性。 缺點 Wilcoxon符號秩檢驗只能用于成對數據的比較,不能處理獨立組或多組比較問題。與配對t檢驗相比,當數據接近正態分布時,該方法的統計效能較低。 應用場景 Wilcoxon符號秩檢驗在蛋白質組學研究中適用于處理時間序列實驗或配對樣本比較的情況。常見應用包括分析同一組樣本在藥物處理前后的蛋白質豐度變化,或同一批樣本在不同時間點的蛋白質表達水平差異。 2.3、Kruskal-Wallis檢驗 原理 Kruskal-Wallis檢驗是Mann-Whitney U檢驗的擴展,適用于三個或更多獨立組的比較。它是單因素方差分析(ANOVA)的非參數對應方法,適用于數據不服從正態分布或方差不齊的情況。該檢驗通過比較各組樣本的秩值,來判斷它們是否來自相同的分布。 優點 Kruskal-Wallis檢驗能夠比較三個或更多組的樣本分布差異,適合多組實驗設計。與單因素ANOVA不同,該檢驗不要求數據服從正態分布,也不需要方差齊性。該方法在處理不對稱分布或包含異常值的數據時表現良好。 缺點 Kruskal-Wallis檢驗只能指出是否存在組間差異,但無法識別具體哪些組之間存在顯著差異。后續需要進行多重比較檢驗。與ANOVA相比,當數據接近正態分布時,Kruskal-Wallis檢驗的統計效能較低。 應用場景 Kruskal-Wallis檢驗適用于蛋白質組學中涉及多組獨立樣本的實驗設計。例如,比較不同藥物劑量或不同時間點對蛋白質豐度的影響,或者分析多個實驗條件下蛋白質的表達水平變化。
三. 多重檢驗校正(Multiple Testing Correction)
原理 在蛋白質組學研究中,研究者通常需要同時對成千上萬個蛋白質進行顯著性檢驗。為了控制假陽性率,必須進行多重檢驗校正。常用的多重檢驗校正方法有Bonferroni校正和Benjamini-Hochberg(BH)校正。 Bonferroni校正:將顯著性水平α除以檢驗次數,以嚴格控制假陽性率。它雖然有效,但過于嚴格,可能導致錯失真正的顯著結果。 Benjamini-Hochberg校正:通過控制假發現率(FDR),提供了在較低假陽性率的同時保留更多顯著結果的方法,因此被廣泛應用。 優點 多重檢驗校正能夠有效減少蛋白質組學研究中的假陽性結果,確保分析結果的可靠性。 缺點 過于嚴格的校正方法(如Bonferroni校正)可能會過度校正,導致錯失真正的顯著結果。而較為靈活的校正方法(如BH校正)雖然能保留更多顯著結果,但假陽性風險較大。 應用場景 在大規模蛋白質組學研究中,尤其是在高通量數據分析時,多重檢驗校可以用于減少因多次檢驗帶來的假陽性結果。